Matriks: matriks

Matriks adalah susunan bilangan real berbentuk empat persegi panjang yang dibatasi oleh tanda kurung "()" atau kurung siku "[ ]"

Jenis-jenis matriks

Matriks Baris

Matriks baris adalah matriks yang terdiri dari satu baris saja.

Contoh :

$\textrm{A} \; = \; \begin{bmatrix} 1 \; 0 \; 0 \end{bmatrix}$

Matriks Kolom

Matriks kolom adalah matriks yang hanya terdiri dari satu kolom saja.

Contoh :

$\textrm{A} \; = \begin{bmatrix} 1\\ 2\\ 3 \end{bmatrix}$

Matriks Nol

Matriks nol adalah matriks yang semua komponennya bilangan nol.

Contoh :

$\textrm{A} \; = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}$

Matriks Identitas

Matriks identitas adalah matriks persegi yang elemen-elemen diagonal utamanya adalah 1, sedangkan yang lainnya nol.

Contoh :

$\textrm{A} \; = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$

Matriks Mendatar

Matriks mendatar adalah adalah matriks yang jumlah kolom lebih banyak dari jumlah baris.

Contoh :

$\textrm{A} \; = \begin{bmatrix} 1 & 2 & 3 & 4 & 5 \\ 6 & 7 & 8 & 9 & 10 \end{bmatrix}$

Matriks Tegak

Matriks tegak adalah matriks yang memiliki jumlah baris lebih banyak dari jumlah kolom.

Contoh :

$\textrm{A} \; = \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \\ 7 & 8 \end{bmatrix}$

Matriks Skalar

Matriks Skalar adalah matriks yang elemen-elemen diagonal utamanya sama, sedangkan elemen lainnya nol.

Contoh :

$\textrm{A} \; = \begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}$

Matriks Diagonal

Matriks diagonal adalah matriks yang elemen-elemen di luar diagonal utamanya nol.

Contoh :

$\textrm{A} \; = \begin{bmatrix} 3 & 0 \\ 0 & 2 \end{bmatrix}$

$\textrm{B} \; = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{bmatrix}$

Matriks Segitiga Atas

Matriks segitiga atas adalah matriks persegi yang elemen-elemen di bawah diagonal utamanya nol.

Contoh :

$\textrm{A} \; = \begin{bmatrix} 2 & 1 \\ 0 & 2 \end{bmatrix}$

$\textrm{B} \; = \begin{bmatrix} 1 & 2 & 3 \\ 0 & 4 & 5 \\ 0 & 0 & 6 \end{bmatrix}$

Matriks Segitiga Bawah

Matriks segitiga bawah adalah adalah matriks persegi yang elemen-elemen di atas diagonal utamanya nol.

Contoh :

$\textrm{B} \; = \begin{bmatrix} 1 & 0 & 0 \\ 2 & 3 & 0 \\ 4 & 5 & 6 \end{bmatrix}$

Matriks Simetri

Matriks simetri adalah matriks persegi yang elemen-elemen di atas diagonal utamanya sama dengan elemen-elemen di bawah diagonal utamanya.

Contoh :

$\textrm{A} \; = \begin{bmatrix} 2 & 3 \\ 3 & 2 \end{bmatrix}$

$\textrm{B} \; = \begin{bmatrix} 1 & 2 & 4 \\ 2 & 3 & 5 \\ 4 & 5 & 6 \end{bmatrix}$

Matriks Transpose

Transpose matriks A disimbolkan dengan $A^{T}$ . Matriks transpose adalah matriks yang diperoleh dengan cara menukar elemen pada baris menjedi elemen pada kolom.

Matriks transpose memiliki sifat-sifat yaitu,

$\left( A + B \right) ^{T} = A^{T} + B^{T}$

$\left( A^{T} \right)^{T} = A$

$(k \cdot A)^{T} = k \cdot A^{T}$

$(AB )^{T} = B^{T} A^{T}$

Contoh :

Operasi Aritmatik Matriks

Kesamaan 2 Matriks

2 matriks dikatakan sama jika ordonya sama dan elemen yang seletak sama.

Contoh :

$\begin{pmatrix} 2 & 3 & 5 \\ 1 & 4 & -7 \end{pmatrix} = \begin{pmatrix} 2 & 6x & z-y \\ 2y+2 & 4 & -7 \end{pmatrix}$

Tentukan nilai x, y, dan z

Jawab :

6x = 3 2y + 2 = 1 z - y = 5

x = 3/6 2y = -1 z -(-1/2) = 5

x = 1/2 y = -1/2 z = 9/2

Penjumlahan Matriks

2 matriks bisa dijumlahkan jika ordonya sama dan penjumlahan dilakukan dengan cara menjumlahkan elemen yang seletak.

Contoh :

$\begin{pmatrix} 2 & 3 & 5 \\ 1 & 4 & -7 \end{pmatrix} + \begin{pmatrix} 2 & 6x & z-y \\ 2y+2 & 4 & -7 \end{pmatrix} = \begin{pmatrix} 4 & 3+6x & 5+z-y \\ 2y+3 & 8 & -14 \end{pmatrix}$

Pengurangan Matriks

2 matriks bisa dikurangkan jika ordonya sama dan pengurangan dilakukan dengan cara mengurangkan dari elemen yang seletak.

Contoh :

$\begin{pmatrix} 2 & 3 & 5 \\ 1 & 4 & -7 \end{pmatrix} - \begin{pmatrix} 2 & 6x & z-y \\ 2y+2 & 4 & -7 \end{pmatrix} = \begin{pmatrix} 0 & 3-6x & 5-z-y \\ -2y-1 & 0 & 0 \end{pmatrix}$

Perkalian Bilangan dengan Matriks

Contoh :

$3 \begin{pmatrix} 2 & 6x & z-y \\ 2y+2 & 4 & -7 \end{pmatrix} = \begin{pmatrix} 6 & 18x & 3z-3y \\ 6y+6 & 12 & -21 \end{pmatrix}$

Perkalian Matriks

2 Matriks dapat dikalikan jika jumlah baris matriks A = jumlah kolom matriks B.

Misal :

$A= \begin{pmatrix} a & b \\ c & d \end{pmatrix}$ dan $B= \begin{pmatrix} p & q \\ r & s \end{pmatrix}$ maka $A \times B= \begin{pmatrix} ap+br & aq+bs \\ cp+dr & cq+ds \end{pmatrix}$

Contoh :

$\begin{pmatrix} 2 & 6 \\ 3 & 4 \end{pmatrix} \begin{pmatrix} 9 & 8 \\ 2 & 10 \end{pmatrix} = \begin{pmatrix} 30 & 76 \\ 35 & 64 \end{pmatrix}$

Determinan Matriks

Matriks Ordo 2x2

misal :

$A= \begin{pmatrix} a & b \\ c & d \end{pmatrix}$ maka Determinan A (ditulis

\left\vert A \right\vert

) adalah: $\left\vert A \right\vert= a \times d - b \times c$

Matriks Ordo 3x3

Cara Sarrus :

misal :

$A= \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix}$ , tentukan

\left\vert A \right\vert

jawab :

$\left\vert A \right\vert = \left\vert \begin{matrix} a & b & c \\ d & e & f \\ g & h & i \end{matrix} \right\vert \begin{matrix} a & b \\ d & e \\ g & h \end{matrix}$ lalu $\left\vert A \right\vert = a.e.i + b.f.g + c.d.h - g.e.c - h.f.a - i.d.b$

Contoh :

$A= \begin{pmatrix} -2 & 0 & 1 \\ 3 & 2 & -1 \\ 1 & -3 & 5 \end{pmatrix}$ maka tentukan

\left\vert A \right\vert

$\left\vert A \right\vert = \left\vert \begin{matrix} -2 & 0 & 1 \\ 3 & 2 & -1 \\ 1 & -3 & 5 \end{matrix} \right\vert \begin{matrix} -2 & 0 \\ 3 & 2 \\ 1 & -3 \end{matrix}$

$\left\vert A \right\vert = (-2.2.5) + (0.-1.-1) + (1.3.-3) - (1.2.1) - (-2.-1.-3) - (0.3.5) = -20+0-9-2+6-0 = -25$

Cara Ekspansi Laplace
Metode ini menggunakan bantuan determinan matriks 2x2 yang terbentuk dari pencoretan baris ke i dan kolom ke j. Kita dapat memilih akan mengekspansi ke arah yang kita mau, bisa searah baris ke i bisa juga searah kolom ke j. Contohnya dengan matriks A yang sama dengan contoh di atas dan kita ekspansi searah dengan baris 1.
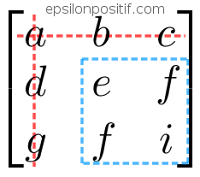
Ekspansi Baris

misal :

contoh soal :
Hasil gambar untuk determinan matriks metode laplace

Matriks

Jumat, 14 September 2018

matriks

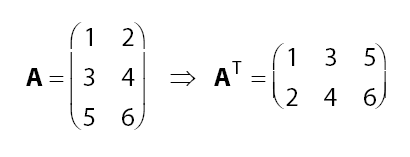
Tidak ada komentar:

Posting Komentar